Why regularization reduces overfitting
Training table
| High bias?(underfitting) | High variance?(overfitting) | |
| yes | - Bigger Network (more hidden unit and layer) - Train longer | - More data - Regularization |
| no | - Check whether High variance | - Done |
This table is telling what you need to do your model when there are underfitting or overfitting. Underfitting is that your model doesn't learn the data set well. In this case, your model predicts the expectation very roughly. i.e. accuracy from train data is bigger than your thought. So you need to do something that modifies your model to train the data in more detail. Expanding your neural net and increasing the number of iteration will help allay this.
Overfitting is the opposite situation. This is the case that your model fits too much to the train data so not quite good to work with the test data. In other words, this model even learns the noisy data in the train data set. i.e. accuracy from train data >> accuracy from test data. To overcome, an easy way is to get more data. But it is expansive to get and compute. So we will use regularization instead of getting more data.
what is regularization and why does it work?
the basic mechanism is simple. Adding some parameter at the end of the loss function, It would help to prevent the overfitting as well as to make a good prediction. I've searched many times to find a basic principle of mechanism in regularization. I couldn't find any clear answer but a paper that is dealing with the mechanisms of weight decay regularization[2]. According to the paper, We could see that regularization improves the model's performance. So we could apply regularization to the model on faith with experimental empiricism. Because Machine learning is a highly empirical process. But I have a plausible hypothesis about why regularization works. Let me show you.
Why L2 Regularization does reduce overfitting.
L2 Regularization will make the weights shrink. It is to prevent overfitting from your neural network. But why? Let's take a look at the equation of L2 Regularization.
(1) is cost function. (2) is cost function and L2 Regularization. I don't see how that equation to make an impact yet. Then how about updating weight from those equations?
As you can see, updating the weight equation from (2) is more subtracting from the weight than from (1) which means the lambda(regularization hyperparameter) in (b) is getting larger, the W is getting smaller. then Z[l] is also going to be smaller.
So what is going to happen? Let us assume that we are using tanh function as the activation function.
 |
| X-axis = Z , Y-axis = A |
This is a tanh function plot. And as it appears, it is a non-linear function. But if we zoom in on close to 0, it'd look like a linear function. So I'd like to say that it has the aspect of a linear function. This is a tip for how to prevent overfitting by the regularization hyperparameter. the reason why we are using non-linear functions as activation function is to train more data detailedly. And sometimes it is fitting too detailedly so it trains any noisy data as best and causes overfitting problems. Then what if we can manipulate the value Z to converge on close to zero? What I mean is, why don't we take the aspect of a linear function from one of the non-linear functions such as tanh function?
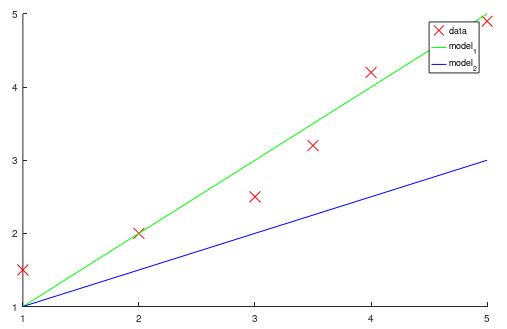
To review the equation (b), when Lamba equals zero, that is identical with the equation (a). As you can see, the plot without hyperparameter that means lambda is zero was overfitted to the data. That is not what you want to your model be. So I tried to reduce the overfitting adding hyperparameter lambda to updating equation and the left side is the result. It's cool. What I only did to my train model is to turn 0 contained in lambda into 0.1. That's all I did and it solves the overfitting problem.
There are several ways to regularize your model. So let me let you find the others and apply those to your model. It will be fun. I hope you enjoy my post and if you see any missing or error in this post, let me know.
Kaggle notebook
references
[2]Guodong Zhang, Chaoqi Wang, Bowen Xu, Roger Grosse, THREE MECHANISMS OF
WEIGHT DECAY REGULARIZATION, University of Toronto, Vector Institute




Comments
Post a Comment