Cost Function and Gradient Descent
Cost function
What is the Cost function? According to Wikipedia, Cost function (or Loss function) is used to minimize the loss. Okay, then the next question is What is the loss? In terms of data science, the loss stands for loss of information. For example. simply, Let's say you designed a machine that measures temperature. If the machine says the outdoor temperature is 25 degrees and actually it is 27 degrees, the machine makes a loss of information. The smaller loss, The more reliability. In the process to reduce a loss, we can use cost function. Let's take a look more detailed example.
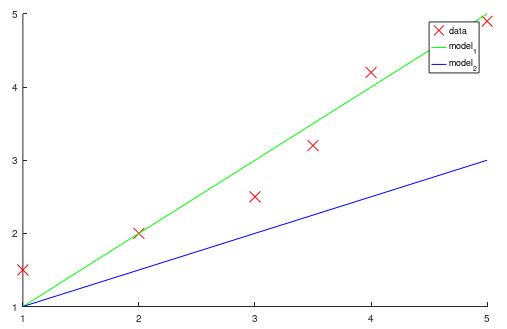
As we can see in this plot, red 'X' is data and the blue and green linear lines are models. You can think of the lines as models to predict the data. Intuitively, the green line is closer to the data than the blue line. But you may not want to work with your intuition only. Moreover, in the real-world, data and model won't be so easy to recognize which one is better than others at a glance. So we bring the cost function for this moment.
Mean Square Error
Mean Square Error is one of the cost functions that measure the loss. Let me bring a simple data set.
- Real data: [1, 2, 3]
- Prediction_1: [0.5, 2, 3.5]
- Prediction_2: [0,8 1.8, 3.3]
- y_i: prediction value.
- t_i : Target value (real data)
- n: The number of data
applied with this equation to the simple data,
According to the calculation, Prediction_2 is closer to the data than Prediction_1. Because the error value from Prediction_2 is smaller than Prediction_1 which means Prediction_2 has less loss of information. So to choose the model that has a small value of the cost function is reasonable. This is just an easy version in order to understand how cost function works. Because we compared only two predictions with only three data. In the real world, there are a lot of cases that have more features and data.
Okay. Now we know that what cost function is and to choose the model which has the minimum value of cost function is the best. Then the next question that would pop up in your mind is how to find the minimum value of cost function. Right in this stage, we need to know about Gradient Descent.
Gradient Descent
To unbox Gradient Descent, we need to have a concept of the derivative. Yes, this is not a math class and also math was never my best subject while the whole my school life. So I just want to give a bit of concept of the derivative.
We can think of the derivative as a tendency. If something goes up, It is a growing trend and It is a positive value in terms of the derivative of something.
That is it. We are just done half the battle of Gradient Descent. As you can see, the point which has the slope is zero is the minimum value of the red line. So what we only have to do is to find the point of zero slopes then we would get the minimum value of a function.
Why do we find the zero slope point?
To answer this question, we need to define what function is a matter to consider. I want you to think of the plot above as a function plot about a loss. i.e. the higher points on the plot stand for the great value about loss. You may remember that our purpose is to minimize the cost so we are able to get the best fit model. The easiest way to find the minimum values on a plot is to find a point which of a slope value is zero. But beware of that the slope values of maximum values on a plot are also zero and it is possible there are several zero-slope-points. Therefore, for now, let us play with the only case of linear regression. Because the shape of the cost function from linear regression is always convex which means there is only one minimum zero slope point.
Of course, if you are a derivative expert or a major in mathematics, it would be drowned in your mind easily. But I think understanding a concept without difficult equations is enough to use these on your problem. Thank you to read it and I hope you enjoyed this posting
references

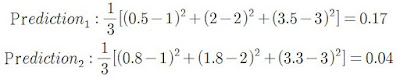


Comments
Post a Comment